MANTIK TARİHİ
Mantığın tarihçesi, eski zamanlarda Hindistan, Çin ve Yunanistan’da gelişmesiyle başlar. Antik Yunanlıların mantık yöntemleri, özellikle Organon’da bulunan Aristoteles mantığı (veya terim mantığı), Batı biliminde ve matematiğinde binlerce yıldır geniş uygulama ve kabul gördü. [1] Stoacılar, özellikle chrysippus yüklem mantığı gelişimine katkıda bulundu.
Boethius, İbni Sina ve William of Ockham gibi Hıristiyan ve İslami filozoflar, Aristoteles‘in mantığını Orta Çağ’da daha da geliştirerek on dördüncü yüzyılın ortalarında Jean Buridan ile zirveye ulaştı.[2] Ampirik yöntemler kanıtlandığı gibi, Francis Bacon 1620 tarihinde kaleme aldığı Novum Organonile oldu.
Mantık, 19. yüzyılın ortalarında, konunun, matematikte kullanılan kesin ispat yöntemini örnek alan sıkı ve biçimsel bir disipline dönüştüğü devrimci bir dönemin başlangıcında yeniden canlandı ve Yunan geleneğine geri döndü. [3] Bu dönemde modern “sembolik” veya “matematiksel” mantığın Boole, Frege, Russell ve Peano gibiler tarafından geliştirilmesi, iki bin yıllık mantık tarihindeki en önemli olanıdır ve insan entelektüel tarihindeki en önemli ve dikkate değer olaylardan birisi haline gelmiştir. [4]
Yirminci yüzyılın ilk birkaç on yılında, özellikle Gödel ve Tarski’nin çalışmalarından kaynaklanan matematiksel mantıktaki ilerleme, özellikle 1950’lerden itibaren, modal mantık, zamansal mantık gibi konularda analitik felsefe ve felsefi mantık üzerinde önemli bir etkiye sahipti, deontik mantık ve alaka düzeyi mantığı başlıklarında ilerlemeler görülmüştür.
DOĞU’DA MANTIK
HİNDİSTAN’DA MANTIK
Mantık, eski Hindistan’da bağımsız olarak başladı ve Yunan mantığından bilinen herhangi bir etki olmaksızın erken modern zamanlara doğru gelişmeye devam etti.[5] Medhatithi Gautama (MÖ 6. yüzyıl) anviksiki mantık okulunu kurdu.[6] Mahabarata (12.173.45), 5. yüzyılda, yaklaşık belirtmektedir. Pāṇini (MÖ 5. yüzyıl), Sanskrit dilbilgisi formülasyonu için (Boole mantığının bazı benzerliklere sahip olduğu) bir mantık biçimi geliştirdi. Mantık tarafından açıklanmıştır Chanakya (MÖ 350-283) onun içinde Arthashastra bağımsız bir araştırma alanı olarak gelişir. [7]
Altı Hint düşünce okulundan ikisi olan Nyaya ve Vaisheshika mantıkla ilgilenlerdendir. Nyaya Sutraları ait Aksapada Gautama (c. 2. yüzyıl) Nyaya okul, altı Ortodoks okullarından biri çekirdek metinleri oluşturan Hindu felsefesidir. Bu gerçekçi okul, bir başlangıç önermesi, bir neden, bir örnek, bir uygulama ve bir sonucu içeren beş üyeli katı bir çıkarım şeması geliştirdi. [8] İdealist Budist felsefesi Naiyayikas için baş rakibi oldu. Madhyamika’nın kurucusu Nagarjuna (yaklaşık MS 150-250 “Orta Yol”), bir önermenin 4 olasılığının her birinin sistematik olarak incelenmesini ve reddedilmesini içeren “dört köşeli” bir argümantasyon sistemi olan catuṣkoṭi (Sanskrit) olarak bilinen bir analiz geliştirdi “P” :
- P; yani olmak.
- P değil; yani, olmamak.
- P değil, P; yani olmak ve olmamak.
- değildir (P ya da P); yani ne olmak ne de olmamak.
Önerme mantığı altında, De Morgan’ın yasaları, bunun üçüncü duruma (P ve P değil) eşdeğer olduğunu ve dolayısıyla gereksiz olduğunu ima eder aslında dikkate alınması gereken sadece 3 vaka var.
Ancak, Hintli filozof Dignaga’nın (MS 480-540) bazen resmi bir tasımı geliştirdiği düşünülür [9] ve onu ve onun halefi olan Dharmakirti, Budist mantık zirvesine ulaştı. Analizlerinin gerçekten resmi bir kıyas sistemi oluşturup oluşturmadığı tartışılmaktadır. Özellikle, analizleri, değişmez eşzamanlılık veya yaygınlık olarak da bilinen, çıkarım gerektiren bir ilişki olan “vyapti” nin tanımına odaklandı. [10] Bu amaçla, “apoha” veya farklılaşma olarak bilinen bir doktrin geliştirildi.[11] Bu, tanımlayıcı özelliklerin dahil edilmesi ve dışlanması olarak adlandırılabilecek şeyi içeriyordu.
Dignāga’nın ünlü “akıl çarkı” (Hetucakra), bir şeyin (duman gibi) başka bir şeyin (ateş gibi) değişmez bir işareti olarak alınabildiğini, ancak çıkarımın genellikle tümevarımcı olduğunu ve geçmiş gözlemlere dayandığını gösterme yöntemidir. Matilal, Dignāga’nın analizinin, John Stuart Mill’in tümevarımsal olan Ortak Anlaşma ve Farklılık Yöntemi’ne çok benzediğini belirtir. [12]
Ek olarak, geleneksel beş üyeli Hint kıyaslaması, tümdengelimsel olarak geçerli olsa da, mantıksal geçerliliği için gereksiz tekrarlara sahiptir. Sonuç olarak, bazı yorumcular geleneksel Hint kıyaslamasını dünyanın pek çok kültüründe tamamen doğal olan ve yine de mantıksal bir biçim olarak görmeyen retorik bir biçim olarak görüyorlar ki mantıksal olarak gereksiz unsurların uğruna ihmal edilmesi anlamında değildir.
ÇİN’DE MANTIK
Çin, çağdaş olarak Konfüçyüs, Mozi, “Usta Mo” kurduğu söylenerek, Mohist okulu olan kanonlar geçerli çıkarım ilişkin konular ve doğru sonuçların koşulları ele almıştır. Özellikle, Mohizm’den doğan okullardan biri olan Mantıkçılar, bazı bilim adamları tarafından biçimsel mantığı erken araştırmaları için itibar görmektedir. Sonraki Qin Hanedanlığı’nda ki yasallığın sert kuralı nedeniyle, bu araştırma hattı, Budistler tarafından Hint felsefesinin tanıtılmasına kadar Çin’de kayboldu.
BATIDA MANTIK
MANTIĞIN TARİH ÖNCESİ DÖNEMİ
İnsanlık tarihinin her döneminde geçerli akıl yürütme uygulanmıştır. Bununla birlikte, mantık geçerli muhakeme, çıkarım ve gösterme ilkelerini inceler. Muhtemelen bir sonucu gösterme fikri, başlangıçta “arazi ölçümü” ile aynı anlama gelen geometri ile bağlantılı olarak ortaya çıktı.[13] Mısırlılar keşfettikleri geometri ile[14] Antik Babil ise matematikte de yetenekliydi. Esagil-kin-apli’nin MÖ 11. yüzyılda tıbbi Teşhis El Kitabı bir dizi mantıksal aksiyomlara ve varsayımlara dayanıyordu. [15] Babil astronomları ise MÖ 8 ve 7. yüzyıllarda gezegen sistemlerine yaptıkları katkı ile bilim felsefesinde yerlerini almaktaydı. [16]
ARİSTOTALES’TEN ÖNCE ANTİK YUNANİSTAN
Eski Mısırlılar, geometrinin bazı gerçeklerini deneysel olarak keşfetmiş olsalar da, eski Yunanlıların büyük başarısı, deneysel yöntemlerin yerini kanıtlayıcı kanıtlarla değiştirmekti. Hem Thales ve Pisagor ait Sokrates öncesi filozofların geometrilerinin yöntemlerinin farkında görünüyor.
Erken kanıtların parçaları Platon ve Aristoteles‘in [17] eserlerinde korunmuştur ve tümdengelim sistemi fikri muhtemelen Pisagor okulunda ve Platon Akademisinde biliniyordu.[14] İskenderiye Öklidinin ispatları Yunan geometrisinin bir paradigmasıdır. Geometrinin üç temel ilkesi aşağıdaki gibidir:
- Bazı önermelerin ispat edilmeksizin doğru olduğu kabul edilmelidir; böyle bir önerme, geometri aksiyomu olarak bilinir.
- Bir geometri aksiyomu olmayan her önerme, geometri aksiyomlarından şu şekilde gösterilmelidir ki böyle bir gösteri, önermenin bir kanıtı veya “türetilmesi” olarak bilinir.
- Kanıt resmi olmalıdır; yani, önermenin türetilmesi söz konusu özel konudan bağımsız olmalıdır. [14]
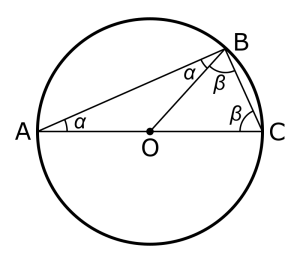
Thales Teoremi
İlk Yunan düşünürlerinin akıl yürütme ilkeleriyle ilgilendiğine dair daha fazla kanıt, muhtemelen MÖ dördüncü yüzyılın başında yazılan dissoi logoi adlı parçada bulunur. Bu, hakikat ve yanlışlık hakkında uzun süreli bir tartışmanın parçasıdır.[18] Klasik Yunan şehir devletlerinin durumunda, tartışma da ilgi faaliyetleri ile uyarılmış retorikçileri veya hatipler ve sofistlerinin savunmak veya hukuki ve siyasi bağlamlarda bir tez, hem saldırmak için argümanlar kullanılmıştır. [19]
Thales
Thales, Yunan felsefesin ilklerinden kabul edilirken, [20] [21] tıpkı Pisagor’un Pisagor teoremine sahip olması gibi, Thales’in de Thales teoremini keşfetmiştir. [22]
Thales, teoremine dört sonuç çıkararak geometriye uygulanan tümdengelimli akıl yürütmeyi kullanan bilinen ilk kişi ve matematiksel bir keşfin atfedildiği bilinen ilk kişidir.[23] Hintli ve Babil matematikçiler onun özel durumlar için teoremini kanıtlamadan önce biliyorlardı.[24] Thales’in Babil’e yaptığı seyahatlerde yarım daire içine yazılmış bir açının dik açı olduğunu öğrendiğine inanılmaktadır. [25]
Pisagor
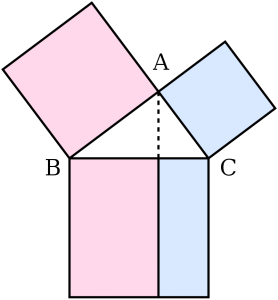
Öklid Unsurlarında Pisagor Teoreminin Kanıtı
MÖ 520’den önce, Mısır veya Yunanistan’a yaptığı ziyaretlerden birinde Pisagor, Thales’ten 54 yaş küçüktü.[26] Sistematik ispat araştırması, MÖ 6. yüzyılın sonlarında Pisagor okuluyla (yani Pisagorlular) başlamış gibi görünmektedir. [14] Nitekim, her şeyin sayı olduğuna inanan Pisagorcular, maddeden ziyade biçimi vurgulayan ilk filozoflardı. [27]
Herakleitos ve Parmenides
Herakleitos’un yazısı (yaklaşık 535 – MÖ 475), logo kelimesine antik Yunan felsefesinde özel önem verildiği ilk yerdi. [28] Herakleitos her şeyin değiştiğini ve her şeyin ateş ve çelişkili zıtlıklar olduğunu, görünüşte sadece birleşik olduğunu savundu. bu Logos tarafından. Belirsiz sözleriyle tanınır.
“Bu logolar her zaman geçerlidir, ancak insanlar onu hem duymadan önce hem de ilk duyduklarında her zaman anlayamadıklarını kanıtlarlar. Çünkü her şey bu logoya uygun hale gelse de insanlar benim yola çıktığım gibi bu tür söz ve eylemleri deneyimlediklerinde deneyimsizler gibidir, her birini doğasına göre ayırır ve nasıl olduğunu söyler. Ancak diğer insanlar, uyurken yaptıklarını unuttukları gibi, uyanık olduklarında da ne yaptıklarını fark edemezler.”

Parmenides, mantığın keşfi olarak adlandırıldı.
Herakleitos’un aksine Parmenides, her şeyin bir olduğunu ve hiçbir şeyin değişmediğini savundu. Muhalif bir Pisagorcu olabilirdi, Bir’in (bir sayı) çoğunu ürettiği konusunda hemfikir değildi. [29] “X değildir” her zaman yanlış veya anlamsız olmalıdır. Var olan hiçbir şekilde var olamaz. Üretimi ve yıkımı fark eden duyu algılarımız büyük bir yanılgı içindedir. Parmenides, duyu algısı yerine logoları Hakikat aracı olarak savundu. O, mantığın keşfi olarak anıldı. [30] [31]
- Bu görüşe göre, Var Olmayan, asla üstün olamaz. Düşüncenizi bu arayıştan alıkoymalısınız, ya da çeşitliliğindeki sıradan deneyimin sizi bu şekilde zorlamasına izin vermemelisiniz (yani izin verme), olduğu gibi kör olan göz ve ses dolu kulağı ve dili. yönetmek; ama benim tarafımdan açıklanan çok tartışmalı kanıtı Sebep ( Logolar ) aracılığıyla yargılamak (zorundasın) (B 7.1–8.2)
Parmenides’in öğrencisi Elealı Zeno, redüktio ad absurdum olarak bilinen ispat yönteminde bulunan standart bir argüman modeli fikrine sahipti. Bu, bir varsayımdan açıkça yanlış (yani, “saçma”) bir sonuç çıkarma, böylece varsayımın yanlış olduğunu gösterme tekniğidir. [32] Bu nedenle, Zeno ve öğretmeni mantık sanatını ilk uygulayanlar olarak görülüyor. [33] Plato diyalog Parmenides savunan bir kitap yazdım iddia olarak Zeno tasvir monizm birden fazla olduğunu varsayarak saçma sonucu göstererek Parmenides’in. Zeno, harekete karşı argümanlarında paradokslarını geliştirmek için bu yöntemi ünlü bir şekilde kullanmıştır. Böyle diyalektik akıl yürütme daha sonra popüler oldu. Bu okulun üyelerine “diyalektikçiler” deniyordu (Yunanca “tartışmak” anlamına gelen bir kelimeden).
Platon
“Geometriden habersiz kimsenin buraya girmesine izin vermeyin.”
- Platon Akademisi girişinin üzerine yazılmış.

Platon Akademisi mozaiği
Büyük dördüncü yüzyıl filozofu Platon’un (MÖ 428-347) hayatta kalan çalışmalarının hiçbiri herhangi bir biçimsel mantık içermiyor [34], ancak felsefi mantık alanına önemli katkılar içeriyor. Platon üç soruyu gündeme getiriyor:
- Doğru veya yanlış olarak adlandırılabilecek şey nedir?
- Geçerli bir argümanın varsayımları ile sonucu arasındaki bağlantının doğası nedir?
- Tanımın doğası nedir?
İlk soru, Platon’un düşünce veya görüşü konuşma veya söylemle (logolar) tanımladığı Theaetetus diyalogunda ortaya çıkar. [35] İkinci soru, Platon’un Formlar teorisinin bir sonucudur. Formlar, sıradan anlamdaki şeyler ya da zihindeki katı fikirler değildir, ancak filozofların daha sonra evrensel dedikleri şeye karşılık gelirler, yani aynı ada sahip her şey kümesinde ortak olan soyut bir varlık. Hem Cumhuriyet hem de Sofist’te Platon, geçerli bir argümanın varsayımları ile sonucu arasındaki gerekli bağlantının “biçimler” arasındaki gerekli bir bağlantıya karşılık geldiğini öne sürer.[36] Üçüncü soru, tanımla ilgilidir. Platon’un diyaloglarının çoğu, bazı önemli kavramların (adalet, hakikat, İyi) bir tanımının araştırılmasıyla ilgilidir ve Platon’un matematikteki tanımın öneminden etkilenmiş olması muhtemeldir. [37] Her tanımın altında yatan şey, farklı tikel şeylerde mevcut olan ortak doğa olan Platonik bir Biçimdir. Dolayısıyla, bir tanım, anlayışın nihai amacını yansıtır ve tüm geçerli çıkarımların temelidir. Bu, Platon’un öğrencisi Aristoteles üzerinde, özellikle de Aristoteles‘in bir şeyin özü mefhumunda büyük bir etkiye sahipti. [38]
ARİSTO

Aristo
Aristoteles‘in mantığı ve özellikle kıyas teorisi Batı düşüncesinde muazzam bir etkiye sahipti.[39] Aristoteles, mantıksal söz diziminin, ismin (veya terimin) ve fiilin sistematik bir analizini deneyen ilk mantıkçıydı. Bir argümanın temelindeki mantıksal biçimini göstermek için değişkenler kullanarak akıl yürütme ilkelerini gösterdiği için ilk resmi mantıkçıydı.[40] Gerekli çıkarımı karakterize eden bağımlılık ilişkilerini araştırdı ve geçerliliği ayırt ettibu ilişkilerin gerçeğinden yola çıkarak. Çelişki ilkeleriyle ilk ilgilenen oydu ve ortayı sistematik bir şekilde dışladı. [41]

Aristoteles’in mantığı hala Rönesans’ta etkiliydi
Organon
Organon adı verilen mantıksal çalışmaları, modern zamanlara kadar inen en eski resmi mantık çalışmalarıdır. Tarihleri belirlemek zor olsa da, Aristoteles‘in mantıksal çalışmalarının olası yazım sırası şöyledir:
- Kategoriler, on tür ilkel terimin incelenmesi.
- Diyalektik tartışması ( On Sophistical Refutations adlı bir ek ile) Konular.
- Yorumlama üzerine, basit kategorik önermelerin basit terimler, olumsuzlama ve nicelik belirtilerine göreanalizi.
- Önceki Analiz, bir kıyaslamayı neyin oluşturduğunun biçimsel bir analizi (Aristoteles’e göre geçerli bir argüman).
- Posterior Analytics, Aristoteles‘in mantık konusundaki olgun görüşlerini içeren bir bilimsel gösteri çalışması.
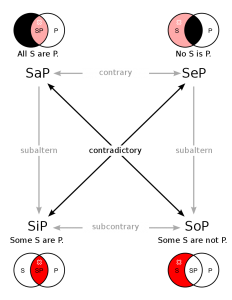
Bu diyagram arasındaki çelişkili ilişkileri gösterir kategorik önermeler içinde muhalefet karesi içinde Aristoteles mantığının.
Bu çalışmalar mantık tarihinde büyük önem taşımaktadır. Gelen Kategoriler, o bir terim başvurabilir hangi olası tüm şeyleri ayırt dener; bu fikir, Batı düşüncesi üzerinde derin bir etkiye sahip olan felsefi çalışması Metaphysics’in temelini oluşturur.
Ayrıca Topics and Sophistical Refutations’da sunulan bir formel olmayan mantık teorisi (yani yanlışlıklar teorisi) geliştirdi. [41]
Yorumlama, muhalefet ve ihtida kavramlarının kapsamlı bir incelemesini içerir; 7. bölüm muhalefet karesinin (veya mantıksal karenin) kökenindedir; Bölüm 9, modal mantığın başlangıcını içerir.
Önceki analizi değişkenler, salt formel tedavinin kullanımı ve bir aksiyomatik sistemin kullanımı: üç önemli ilke tarihinde ilk kez uygulanan “tasım”, onun fuar içeriyor.
STOACILAR
Yunan mantığının diğer büyük okulu Stoacılarınkidir. [42] Stoacı mantığın kökleri, muhtemelen Parmenides ve Zeno geleneğini izleyen, Sokrates’in öğrencisi ve Platon’un biraz daha eski çağdaşı olan MÖ 5. yüzyılın sonlarında filozof Megara’lı Öklid’e dayanır. Gözbebekleri ve ardılları “denirdi Megaralılar ” veya “Eristics” ve daha sonra “diyalektikçidir”. Megaristan okulunun en önemli iki diyalektisti, MÖ 4. yüzyılın sonlarında aktif olan Diodorus Cronus ve Philo idi.

Soli Krizippu
Stoacılar Megar mantığını benimsedi ve sistemleştirdi. Okulun en önemli üyesi, üçüncü başkanı olan ve Stoacı doktrinin çoğunu resmileştiren Chrysippus’du (MÖ 278 – c. 206). Neredeyse hiçbiri hayatta kalmayan mantık üzerine en az 300’ü de dahil olmak üzere 700’den fazla eser yazmış olması gerekiyor.[43] [44] Aristoteles‘in aksine, Megaralıların veya erken dönem Stoacıların tam çalışmalarına sahip değiliz ve çoğunlukla Diogenes Laërtius, Sextus Empiricus, Galen, Aulus Gellius dahil olmak üzere daha sonraki kaynakların hesaplarına (bazen düşmanca) güvenmek zorundayız. Aphrodisiaslı İskender ve Cicero. [45]
Stoacı okulun üç önemli katkısı (i) modalite açıklamaları, (ii) Maddi koşullu teorileri ve (iii) anlam ve hakikat açıklamaları idi. [46]
- Modalite. Aristoteles‘e göre, zamanının Megaralıları, potansiyel ile gerçek arasında hiçbir ayrım olmadığını iddia ettiler. [47] Diodorus Cronus mümkün olanı olan ya da olacak, imkansız olanı doğru olmayacak ve koşullu olanı ya zaten olan ya da yanlış olacak olarak tanımladı. [48] Diodorus ayrıca, aşağıdaki 3 önermenin her bir çiftinin üçüncü önermeyle çeliştiğini belirten Üstün argümanı olarak bilinen şeyle de ünlüdür:
-
- Geçmiş olan her şey doğru ve gereklidir.
- İmkansız, mümkün olandan gelmez.
- Olan ve olmayacak olan şey mümkündür.
- Diodorus, ilk ikisinin akla yatkınlığını, eğer doğru değilse ya da olmayacaksa hiçbir şeyin mümkün olmadığını kanıtlamak için kullandı. [49] Chrysippus, aksine, ikinci önermeyi reddetti ve imkansızın mümkün olandan gelebileceğini söyledi. [50]
- Koşullu ifadeler. Koşullu ifadeleri tartışan ilk mantıkçılar Diodorus ve onun öğrencisi Megara’lı Philo idi. Sextus Empiricus, Diodorus ve Philo arasındaki bir tartışmaya üç kez atıfta bulunur. Philo, hem gerçek bir öncülü hem de yanlış bir sonucu yoksa bir koşulu doğru olarak kabul etti. Kesin olarak, T0 ve T1 doğru ifadeler olsun ve F0 ve F1 yanlış beyanlar olmak; daha sonra Philo’ya göre, aşağıdaki koşulların her biri doğru bir ifadedir, çünkü öncül doğruyken sonucun yanlış olması durumu değildir (yanlış bir ifadenin doğru bir ifadeden geldiği iddia edilmez.):
-
- Eğer T0, daha sonra, T1
- Eğer F0 ise, o zaman T0
- Eğer F0, daha sonra F1
- Aşağıdaki koşul bu koşulu karşılamıyor ve bu nedenle Philo’ya göre yanlış bir ifadedir:
- Eğer T0, daha sonra F0
- Nitekim Sextus, “[Philo] ‘ya göre bir koşulun doğru olabileceği üç yol vardır ve biri yanlış olabilir.” [51] Philo’nun hakikat ölçütü, şimdi “eğer… o zaman” ın hakikat-işlevsel tanımı olarak adlandırılacak olan şeydir ; modern mantıkta kullanılan tanımdır.
- Aksine, Diodorus koşullu ifadelerin geçerliliğine, yalnızca önceki cümle hiçbir zaman gerçek olmayan bir sonuca varamayacağı zaman izin verdi. [51] [52] [53] Bir asır sonra, Stoacı filozof Chrysippus hem Philo hem de Diodorus’un varsayımlarına saldırdı.
- Anlam ve gerçek. Megarian-Stoic mantık ile Aristoteles mantığı arasındaki en önemli ve çarpıcı fark, Megarian-Stoic mantığının terimlerle değil önermelerle ilgili olması ve dolayısıyla modern önermesel mantığa daha yakın olmasıdır.[54] stoacılar söyleyiş (arasında ayırt telefon gürültü olabilir), söz “lexis” ifade olduğu ama anlamsız ve söylem (olabilen) logolar anlamlı ifade olduğu). Teorilerinin en orijinal kısmı, lekton adı verilen bir cümle ile ifade edilenin gerçek bir şey olduğu fikridir; bu, şimdi bir önerme olarak adlandırılan şeye karşılık gelir. Sextus, Stoacılara göre üç şeyin birbirine bağlı olduğunu söyler: Gösteren, gösterilen ve nesne; örneğin, gösteren Dion kelimesidir ve gösterilen, Yunanlıların anladığı, ancak barbarların anlamadığı şeydir ve nesne Dion’un kendisidir. [55]
ORTAÇAĞ’DA MANTIK
İSLAM DÜNYASINDA MANTIK

Avicennian mantığının kurucusu Avicenna’dan bir metin
El-Kindi, Farabi, İbn Sina, Gazali, İbn Rüşd’ün ve diğer Müslüman mantıkçıları, Aristo‘nun mantığa dayalı ve Ortaçağ Batı antik dünyanın fikirleri iletilmesinde önemli bir aracıydılar. [56]
Farabi (Alfarabi) (873-950), gelecekteki olasılıklar konularını, kategorilerin sayısını ve ilişkisini, mantık ile gramer arasındaki ilişkiyi ve Aristotelesçi olmayan çıkarım biçimlerini tartışan Aristotelesçi bir mantıkçıydı.[57] Farabi ayrıca koşullu kıyas teorilerini ve Aristotelesçiden ziyade Stoik mantık geleneğinin bir parçası olan analojik çıkarımlara başvurmuştur. [58]
İbn Sina (980-1037), İslam dünyasında egemen mantık sistemi olarak Aristoteles mantığının yerini alan [59] ve Albertus Magnus gibi Batılı ortaçağ yazarları üzerinde önemli bir etkiye sahip olan kendine has mantığının kurucusuydu. [60] İbn Sina, her ikisi de Stoacı mantık geleneğinin bir parçası olan varsayımsal kıyas [61] ve önermeler hesabı üzerine çalışmalar yazdı.[62] Zamansal mantık ve modal mantığı içeren orijinal bir “zamansal olarak modalize edilmiş” kıyas teorisi geliştirdi. [57] Ayrıca tümevarım mantığından da yararlandı gibi bir anlaşma, farklılık, ve eşlik eden varyasyon yöntemleri için kritik olan bilimsel yöntem. [61] İbn Sina‘nın fikirlerinden biri, Ockham’lı William gibi Batılı mantıkçılar üzerinde özellikle önemli bir etkiye sahipti. İbn Sina‘nın bir anlam veya kavram için kullandığı kelime (ma’na), skolastik mantıkçılar tarafından, Ortaçağ mantığı ve epistemolojisinde bu, zihinde bir şeyi doğal olarak temsil eden bir işaretti. [63]
Bu, Ockham‘ın kavramsalcılığının gelişimi için çok önemliydi: Evrensel bir terim (ör.“insan”), gerçekte var olan bir şeyi değil, daha çok gerçekte birçok şeyi temsil eden zihinde (intentio in intellectu) bir işaret anlamına gelir. Ockham, bu görüşü desteklemek için Avicenna’nın Metaphysics V hakkındaki yorumundan alıntı yapmıştır. [64]
Fahreddin el-Razi (d. 1149), Aristoteles‘in ” ilk figürünü ” eleştirdi ve John Stuart Mill (1806-1873) tarafından geliştirilen tümevarımsal mantık sisteminin habercisi olan erken bir tümevarım mantığı sistemini formüle etti. [65] El-Razi’nin çalışması daha sonraki İslam alimleri tarafından İslami mantığa, İbni Sina sonrası mantığa doğru yeni bir yön olarak görüldü. Bu, kavramlar ve kabuller meselesi etrafında dönen bir mantık biçimi geliştiren öğrencisi Afdaladdîn el-Khûnajî (ö. 1249) tarafından daha da ayrıntılı hale getirildi. Bu geleneğe cevaben Nasir al-Din al-Tusi(1201–1274), İbn Sina‘nın çalışmalarına sadık kalan ve sonraki yüzyıllarda daha baskın olan Post-Avicennian okuluna bir alternatif olarak var olan bir Neo-Avicennian mantığı geleneğini başlattı. [66]
İşrakilik okul tarafından kurulmuştur Şahab al-Din Suhreverdî’nin tüm yöntemleri (zorunluluk, azaltılması anlamına gelir “kararlı gereklilik” fikrini geliştirdi. (1155-1191) [67]
İbn el-Nafis (1213-1288), İbn-i Sina‘nın Al-Isharat (İşaretler) ve Al-Hidayah’ın (Kılavuz) tefsiri olan Avicennian mantığı üzerine bir kitap yazdı.[68]
İbn Teymiyye (1263–1328), Ar-Radd ‘ala al-Mantiqiyyin’i yazdı, kıyametin geçerliliği olmasa da yararlılığına karşı ve tümevarımsal akıl yürütme lehine tartıştığı yerde.[69][65] İbn Teymiyye, aynı zamanda, tasavvuf argümanlarının kesinliğine karşı ve analoji lehine savundu ve onun argümanı, tümevarıma dayalı kavramların kendilerinin kesin değil, sadece olası olduğudur ve bu nedenle, bu tür kavramlara dayanan bir kıyaslamanın, analojiye dayalı bir argümandan daha kesin olmadığıdır. Ayrıca, tümevarımın kendisinin bir analoji sürecine dayandığını iddia etti. Analojik akıl yürütme modeli, hukuki argümanlara dayanıyordu.[70][71] Bu analoji modeli, John F. Sowa’nın son çalışmasında kullanılmıştır. [71]
Şerhu’l-takmil fi’l-mantiq 15. yüzyılda Muhammed ibn Feyz Allah ibn Muhammed Emin el-Sharwani tarafından yazılmış çalışılmıştır mantığa son büyük Arapça iştir. [72] Bununla birlikte, 14. ve 19. yüzyıllar arasında mantık üzerine “binlerce sayfa” yazılmıştır, ancak bu dönemde yazılan metinlerin yalnızca bir kısmı tarihçiler tarafından incelenmiştir, bu nedenle İslam üzerine orijinal eser hakkında çok az şey bilinmektedir. [66]
ORTAÇAĞ AVRUPASINDA MANTIK

Brito’nun Eski Mantık üzerine soruları
“Ortaçağ mantığı” (aynı zamanda “Skolastik mantık” olarak da bilinir) genellikle ortaçağ Avrupa’sında kabaca 1200-1600 yılları arasında geliştirilen Aristoteles mantığının biçimi anlamına gelir.[1]
Stoacı mantık formüle edildikten sonra yüzyıllar boyunca, klasik dünyadaki egemen mantık sistemiydi. Karanlık Çağlardan sonra mantık çalışması yeniden başladığında, ana kaynak, Aristoteles‘in mantığının bir kısmına aşina olan, ancak Stoacıların neredeyse hiçbir çalışmasına aşina olmayan Hristiyan filozof Boethius’un çalışmasıydı. [73]
On ikinci yüzyıla kadar, Batı’da Aristoteles‘in tek eserleri Kategoriler, Yorumlama Üzerine ve Boethius’un Porphyry’nin İzagogu (Kategoriler üzerine bir yorum) idi. Bu çalışmalar “Eski Mantık” (Logica Vetus veya Ars Vetus) olarak biliniyordu. Bu gelenekteki önemli bir çalışma, Peter Abelard’ın (1079–1142) Logica Ingredientibus’udur. Doğrudan etkisi küçüktü [74], ancak John of Salisbury gibi öğrenciler üzerindeki etkisi harikaydı ve teolojiye titiz mantıksal analiz uygulama yöntemi, takip eden dönemde teolojik eleştirinin gelişimini şekillendirdi. [75]
On üçüncü yüzyılın başlarında, Aristoteles‘in Organon’un kalan eserleri (Ön Analitik, Posterior Analitik ve Sofistik Reddetmeler dahil ) Batı’da kurtarıldı. [76] O zamana kadar mantıksal çalışma, çoğunlukla Aristoteles‘in çalışmaları üzerine yorum veya yorumdan ibaretti. [77] On üçüncü yüzyılın ortalarından on dördüncü yüzyılın ortalarına kadar olan dönem, daha önce gelen Aristoteles geleneğinde çok az temele sahip olan, özellikle orijinal olan üç alanda, mantıktaki önemli gelişmelerden biriydi. Bunlar: [78]
- Varsayım teorisi. Varsayım teorisi, tahminlerin ( örneğin, ‘insan’) bireylerin bir alanı (örneğin, tüm erkekler) üzerindeki menzilini ele alır. [79] ‘Her insan bir hayvandır’ önermesinde, ‘insan’ terimi şu anda var olan erkekler için mi yoksa ‘varsaymak’ mıdır, yoksa bu aralık geçmiş ve gelecekteki erkekleri mi kapsıyor? Var olmayan bir birey için bir terim varsayılabilir mi? Bazı ortaçağ uzmanları, bu fikrin modern birinci dereceden mantığın bir habercisi olduğunu iddia ettiler.[80] ilişkili teorilerle varsayım “teori copulatio (sıfat terimlerin işareti kapasiteli), ampliatio (referans alan genişlemesi) vedağıtım, Batı ortaçağ mantığının en özgün başarılarından birini oluşturur”. [81]
- Syncategoremata teorisi. Syncategoremata mantık için gerekli olan terimlerdir, ancak aksine categorematic terimler, kendi adına delalet yoktur, ancak diğer kelimelerle ‘eş delalet’. Syncategoremata örnekleri ‘ve’, ‘değil’, ‘her’, ‘eğer’ vb.
- Teorisi sonuçları. Bunun bir sonucu varsayımsal, koşullu bir önermedir: ‘eğer… o zaman’ terimleriyle birleştirilen iki önerme. Örneğin, ‘bir adam koşarsa, o zaman Tanrı vardır’ (Si homo currit, Deus est). [82] Tamamen gelişmiş bir sonuçlar teorisi, William of Ockham‘ın Summa Logicae adlı eserinin III. Kitabında verilmiştir. Burada Ockham, sırasıyla modern maddi çıkarım ve mantıksal çıkarıma kabaca eşdeğer olan ‘maddi’ ve ‘biçimsel’ sonuçları birbirinden ayırır. Benzer hesaplar Jean Buridan ve Saksonyalı Albert tarafından verilmiştir.
Bu gelenek içinde son büyük eserleri Mantık (olarak bilinen 1589-1644 John Poinsot ait St Thomas John), Metafizik ilgili tartışmalar ait Francisco Suarez (1548-1617) ve Logica Demonstrativa ait Giovanni Girolamo Saccheri (1667-1733 ).
GELENEKSEL MANTIK
DERS KİTABI GELENEĞİ

Dudley Fenner ‘ın Mantık Sanat (1584)
“Geleneksel mantık” genellikle, ders kitabı gelenek anlamına Antoine Arnauld ‘ler ve Pierre Nicole ‘ın Logic veya Düşünme Sanatı daha iyi olarak bilinen Liman-Royal Logic ile başlar.[83] 1662’de yayınlanan bu eser, on dokuzuncu yüzyıla kadar Aristo‘dan sonra mantık üzerine yapılan en etkili çalışmaydı. [84] Kitap, geniş ölçüde Aristoteles ve ortaçağ terim mantığından türetilen bir çerçeve içinde gevşek bir Kartezyen doktrini (örneğin, önermenin terimlerden ziyade fikirlerin bir birleşimidir) sunar. 1664 ile 1700 arasında sekiz baskı yapıldı ve kitabın bundan sonra önemli bir etkisi oldu. [84] Port-Royal, genişleme ve yoğunluk kavramlarını tanıtır. Hesap önermeler o Locke içinde verir Kompozisyon kelimelerdir. “Sözel önermeler, fikirlerimizi belirtileri, araya [edilir] veya olumlu veya olumsuz cümlelerde ayrılan önerme oluşur.[85]
Dudley Fenner, Aristoteles‘e karşı bir tepki olan Ramist mantığının popülerleşmesine yardımcı oldu. Başka etkileyici eseridir Novum Origanum tarafından Francis Bacon başlığı “yeni aracı” olarak çevirir 1620’den yayımlanan. Bu, Aristoteles‘in Organon olarak bilinen çalışmasına bir referanstır. Bu çalışmada Bacon, “yavaş ve sadık bir çaba ile şeylerden bilgi toplayan ve onu anlamaya getiren” alternatif bir prosedür lehine Aristoteles‘in kıyas yöntemini reddeder.[86] Bu yöntem, tümevarımlı akıl yürütme olarak bilinir, ampirik gözlemden başlayan ve aksiyomları veya önermeleri daha düşük seviyeye indiren bir yöntem; bu alt aksiyomlardan daha genel olanlar indüklenebilir. Örneğin, ısı gibi olağanüstü bir doğanın nedenini bulmak için 3 liste yapılmalıdır:
- Varlık listesi: ısının bulunduğu her durumun listesi.
- Devamsızlık listesi: ısı eksikliği dışında, varlık listesindekilerden en az birine benzeyen her durumun listesi.
- Değişkenlik listesi: ısının değişebileceği her durumun listesi.
Daha sonra, ısının biçim doğası (veya nedeni), mevcudiyet listesindeki her durumda ortak olan ve yokluk listesindeki her durumda eksik olan ve değişkenliğin her durumunda dereceye göre değişen olarak tanımlanabilir. liste.
Ders kitabı geleneğinde diğer eserleri arasında Isaac Watts ‘ın: Ya Aklın Sağ Kullanımı Logick (1725), Richard Whately s’ Mantık (1826) ve John Stuart Mill ‘in Mantık A Sistemini (1843). Sonuncusu geleneğin son büyük eserlerinden biri olmasına rağmen, Mill’in mantığın temellerinin iç gözlemde yattığı yönündeki görüşü[87], mantığın en iyi psikolojinin bir dalı olarak anlaşılacağı görüşünü etkiledi, bu görüş sonraki elli yıla hâkim oldu. özellikle Almanya’daki gelişimi. [88]
HEGEL’İN FELSEFESİNDE MANTIK

Georg Wilhelm Friedrich Hegel
Hegel, Encyclopaedia of the Philosophical Sciences’ın ilk cildi olarak 1817’de yayımlanan, Science of Logic’i daha kısa bir çalışmaya yoğunlaştırdığında, mantığın felsefi sistemi için önemine işaret etti. “Daha Kısa” veya “Ansiklopedi” Mantığı, sıklıkla bilindiği gibi, en boş ve soyut kategorilerden – Hegel “Saf Varlık” ve “Saf Hiç” ile başlar – “Mutlak”, kendisinden önceki tüm kategorileri içeren ve çözen kategori. Başlığa rağmen, Hegel’in Mantığı geçerli çıkarım bilimine gerçekten bir katkı değildir. Hegel, öncüllerden geçerli çıkarım yoluyla kavramlar hakkında sonuçlar çıkarmak yerine, bir kavram hakkında düşünmenin başka bir kavram hakkında düşünmeyi zorunlu kıldığını göstermeye çalışır (“Miktar” kavramı olmadan “Nitelik” kavramına sahip olunamaz); bu zorlama, sözde, bireysel psikoloji meselesi değildir, çünkü neredeyse organik olarak kavramların içeriğinden kaynaklanmaktadır. Amacı “Mutlak” ın rasyonel yapısını – rasyonalitenin kendisinde göstermektir. Düşüncenin bir kavramdan karşıtına ve daha sonra başka kavramlara yönlendirildiği yöntem, Hegelci diyalektik olarak bilinir.
Hegel’in Mantığının ana akım mantıksal çalışmalar üzerinde çok az etkisi olmasına rağmen, etkisi başka yerlerde görülebilir:
- Carl von Prantl ‘ın Abendland içinde Lojik der Geschichte (1855-1867). [89]
- FH Bradley’in Mantık İlkeleri (1883) gibi İngiliz İdealistlerinin çalışması.
- Karl Marx’ın ve Marksizmin çeşitli okullarındaki ekonomik, politik ve felsefi çalışmaları.
MANTIK VE PSİKOLOJİ
Mili ve Frege’nin çalışmaları arasında, mantığın geniş çapta tanımlayıcı bir bilim, muhakemenin yapısının ampirik bir çalışması ve dolayısıyla esasen bir psikoloji dalı olarak ele alındığı yarım yüzyıl uzadı. [90] Örneğin, Alman psikolog Wilhelm Wundt, “psikolojik düşüncenin her zaman daha kapsamlı düşünme biçimi olduğunu” vurgulayarak, “psikolojik düşünce yasalarından mantıki” türetmeyi tartıştı. [91] Bu görüş, dönemin Alman filozofları arasında yaygındı:
- Theodor Lipps, mantığı “belirli bir psikoloji disiplini” olarak tanımladı. [92]
- Christoph von Sigwart, mantıksal gerekliliği, bireyin belirli bir şekilde düşünme dürtüsüne dayandığını anladı. [93]
- Benno Erdmann, “mantıksal yasaların sadece bizim düşüncemizin sınırları içinde geçerli olduğunu” savundu. [94]
Mill’in çalışmasını takip eden yıllarda mantığın baskın görüşü buydu. [95] Mantığa bu psikolojik yaklaşım Gottlob Frege tarafından reddedildi. Ayrıca Edmund Husserl tarafından, “ezici” olarak tanımlanan bir saldırı olan Logical Investigations’ın (1900) ilk cildinde genişletilmiş ve yıkıcı bir eleştiriye maruz bırakıldı. [96] Husserl, psikolojik gözlemlerdeki mantığın temellendirilmesinin, tüm mantıksal gerçeklerin kanıtlanmamış kaldığını ve şüphecilik ve göreliliğin kaçınılmaz sonuçlar olduğunu ima ettiğini güçlü bir şekilde savundu.
Bu tür eleştiriler, “psikoloji” denen şeyi hemen ortadan kaldırmadı. Örneğin, Amerikalı filozof Josiah Royce, Husserl’in eleştirisinin gücünü kabul ederken, psikolojideki ilerlemenin mantıktaki ilerlemeye eşlik edeceğinden “şüphe edemedi” ve bunun tersi de geçerli oldu. [97]
MODERN MANTIĞIN YÜKSELİŞİ
On dördüncü yüzyıl ile on dokuzuncu yüzyılın başı arasındaki dönem büyük ölçüde gerileme ve ihmal dönemiydi ve genellikle mantık tarihçileri tarafından kısır olarak görülüyordu.[2] Mantığın yeniden canlanması, konunun matematikte kullanılan kesin ispat yöntemi olan sıkı ve biçimsel bir disipline dönüştüğü devrimci bir dönemin başlangıcında, on dokuzuncu yüzyılın ortalarında meydana geldi. Bu dönemde modern “sembolik” veya “matematiksel” mantığın gelişimi, 2000 yıllık mantık tarihinde en önemli olanıdır ve tartışmasız insan entelektüel tarihindeki en önemli ve dikkat çekici olaylardan biridir. [4]
Bir dizi özellik olarak aşağıdaki olan eski Aristocu veya geleneksel mantık, burada en önemli modern mantık ayırt:[98] modern mantık, temelde taşı olan işlemin kuralları yalnızca belirlenir şekli olup göre anlam ve matematikte olduğu gibi kullandığı semboller. Pek çok mantıkçı matematiğin “başarısından” etkilendi, çünkü herhangi bir gerçek matematiksel sonuç hakkında uzun süreli bir tartışma yoktu. CS Peirce belirtildiği[99] o halde, bir kesin integrali değerlendirilmesinde bir hata Laplace yaklaşık 50 yıldır devam eden ayın yörüngesiyle ilgili bir hataya yol açtı, hata tespit edildiğinde ciddi bir tartışma olmaksızın düzeltildi. Peirce bunu geleneksel mantığı çevreleyen tartışma ve belirsizlikle ve özellikle metafizikteki akıl yürütmeyle karşılaştırdı.. Gerçekten “kesin” bir mantığın matematiğe, yani “diyagramatik” veya “ikonik” düşünceye bağlı olacağını savundu. “Bu tür yöntemleri izleyenler, şüphelenildikten sonra hızla düzeltilecek olanlar dışında tüm hatalardan kaçacaktır”. Modern mantık aynı zamanda “soyutlayıcı” olmaktan çok “yapıcıdır”; yani, sıradan dilden (veya geçerlilik hakkındaki psikolojik sezgilerden) türetilen teoremleri soyutlamak ve resmileştirmek yerine, formel yöntemlerle teoremler inşa eder, ardından sıradan dilde bir yorum arar. Tamamen semboliktir, yani mantıksal sabitler (ortaçağ mantıkçılarının “syncategoremata” olarak adlandırdığı) ve kategorik terimler bile sembollerle ifade edilir.
MODERN MANTIK
Modern mantığın gelişimi kabaca beş döneme ayrılır: [100]
- Leibniz’den, özellikle Leibniz tarafından mantıksal hesap kavramının tartışıldığı ve geliştirildiği, ancak hiçbir okul oluşturulmadığı ve izole periyodik girişimlerin terk edildiği veya fark edilmediği 1847’ye kadar olan embriyonik dönem.
- Cebirsel süresi gelen Boole ‘s Analiz Schröder’s Vorlesungen. Bu dönemde, daha fazla uygulayıcı ve daha büyük bir gelişim devamlılığı vardı.
- Mantıkçı süresi ile ilgili Begriffsschrift arasında Frege için Principia Mathematica’da arasında Russell ve Whitehead. “Mantıkçı ekol” un amacı, tüm matematiksel ve bilimsel söylemlerin mantığını, tüm matematiksel gerçeklerin mantıksal olduğunu temel bir ilke olarak alarak mantık dışı herhangi bir terminolojiyi kabul etmeyen tek bir birleşik sistemde birleştirmekti. Başlıca mantıkçılar Frege, Russell ve ilk Wittgenstein’dı.[101] Principia ile doruğa ulaşır, daha önceki ilerlemenin önünde bir engel teşkil eden çelişkilerin kapsamlı bir incelemesini ve çözülmeye çalışılmasını içeren önemli bir çalışma.
- Metamathematical dönem gelişimini gördük 1930’lara kadar 1910, metalogic içinde, finitist sisteminde Hilbert ve olmayan finitist sistem Löwenheim ve Skolem, çalışmalarında mantık ve metalogic kombinasyonu Gödel ve Tarski. Gödel’in 1931’deki eksiklik teoremi, mantık tarihindeki en büyük başarılardan biriydi. Daha sonra 1930’larda Gödel, küme teorik inşa edilebilirlik kavramını geliştirdi.
- Dünya Savaşı sonrası dönem, ne zaman matematiksel mantık araştırmaları dört birbiriyle ilişkili ancak ayrı bölüme kollara: modeli teorisi, kanıt teorisi, hesaplanabilirlik teorisi ve küme teorisi ve bunun fikir ve yöntemler etkilemeye başladı felsefesi.
EMBRİYONİK DÖNEM

Leibniz
Çıkarımın tamamen mekanik bir süreçle temsil edilebileceği fikri, eşmerkezli halkalardan oluşan bir sistemle sonuç çıkarmak için (biraz eksantrik) bir yöntem öneren Raymond Llull kadar erken bulundu. Oxford Calculators[102] gibi mantıkçıların çalışmaları, kelimelerde mantıksal hesaplamalar (hesaplamalar) yazmak yerine harfleri kullanma yöntemine yol açtı, örneğin Venedikli Paul tarafından Logica dergisinde kullanılan bir yöntem. Llull’dan üç yüz yıl sonra, İngiliz filozof ve mantıkçı Thomas Hobbes, tüm mantık ve muhakemenin, toplama ve çıkarma matematiksel işlemlerine indirgenebileceğini öne sürdü. [103]Aynı fikir, hem Llull hem de Hobbes’u okumuş olan ve mantığın kombinatoryal bir süreç veya hesapla temsil edilebileceğini savunan Leibniz’in çalışmasında da bulunur. Ancak Llull ve Hobbes gibi o da detaylı veya kapsamlı bir sistem geliştirmeyi başaramadı ve bu konudaki çalışmaları ölümünden çok sonrasına kadar yayınlanmadı. Leibniz, sıradan dillerin “sayısız belirsizliğe” tabi olduğunu ve görevi kelimelerin biçimlerinden ve yapılarından kaynaklanan çıkarımdaki hataları açığa çıkarmak olan bir hesaplama için uygun olmadığını söylüyor; [104] bu nedenle, karmaşık fikirleri ifade etmek için oluşturulabilecek temel kavramları içeren bir insan düşüncesi alfabesi tanımlamayı [105] ve bir hesap oranlayıcı oluşturmayı önerdi.bu, tüm argümanları “Matematikçilerinkiler kadar somut hale getirir, böylece hatamızı bir bakışta bulabiliriz ve kişiler arasında anlaşmazlıklar olduğunda, basitçe şunu söyleyebiliriz: Hadi hesaplayalım.” [106]
Gergonne (1816), muhakemenin, kişinin tamamen açık fikirlere sahip olduğu nesnelerle ilgili olması gerekmediğini, çünkü cebirsel işlemlerin ilgili sembollerin anlamı hakkında herhangi bir fikir sahibi olmadan gerçekleştirilebileceğini söyledi. [107] Bolzano, mantıksal sonucu veya “çıkarılabilirliği” değişkenler açısından tanımlarken modern kanıt teorisinin temel bir fikrini öngördü: [108]
Bu yüzden önerileri söylüyorum … olan deducible önermelerden , , , ,… Değişken parçalarla ilgili olarak , ,…, İkamesi olan her fikir sınıfı , ,… Hepsini yapar , , , ,… Doğru, aynı zamanda , , ,… doğru. Ara sıra, alışılmış olduğu için, önerilerin , , … izleyin, ya da anlaşılmaktadır ya türetilmiş gelen, , , , ,…. Öneriler , , , … Ben diyeceğim binaları, , , ,… Sonuçlar.
Bu artık anlamsal geçerlilik olarak bilinir.
CEBİRSEL DÖNEM

George Boole
Modern mantık dahil Boole ile “cebirsel okulu” menşeli olarak bilinen ve ne ile başlar Peirce, Jevons, Schröder ve Venn.[109] Amaçları, sınıflar, önermeler ve olasılıklar alanında akıl yürütmeyi resmileştirmek için bir hesap geliştirmekti. Okul, Boole’un 1847’de ortaya çıkan Matematiksel Mantık Analizi adlı eseri ile başlar, ancak De Morgan (1847) onun hemen öncüsüdür. [110] Boole sisteminin temel fikri, cebirsel formüllerin mantıksal ilişkileri ifade etmek için kullanılabileceğidir. Bu fikir, Boole’un gençlik yıllarında, özel bir okulda gösterici olarak çalışarak aklına geldi. Lincoln, Lincolnshire. [111]
Örneğin, x ve y, sınıfları temsil etsin, sembol = sınıfların aynı üyelere sahip olduğunu, xy, x ve y’nin tüm ve yalnızca üyelerini içeren sınıfı temsil etmesine izin verin vb. Boole bu seçmeli sembolleri, yani dikkate alınmak üzere belirli nesneleri seçen sembolleri çağırır.[112]
Seçmeli sembollerin kullanıldığı bir ifadeye seçmeli fonksiyon denir ve üyelerin seçmeli fonksiyonlar olduğu bir denklem seçmeli bir denklemdir. [113] Seçmeli işlevler teorisi ve bunların “gelişimi”, esasen modern hakikat işlevleri fikridir ve bunların ayırıcı normal biçimidir. [112]
Boole’un sistemi, sınıf mantığı ve önerme mantığı olmak üzere iki yorumu kabul eder. Kıyas teorisinin konusu olan “birincil önermeler” ile önermeler mantığının konusu olan “ikincil önermeler” arasında ayrım yapan Boole, farklı “yorumlar” altında aynı cebirsel sistemin her ikisini de nasıl temsil edebileceğini gösterdi. Birincil önermeye bir örnek, “Bütün bölge sakinleri ya Avrupalı ya da Asyalı’dır.” İkincil bir önermeye bir örnek, “Ya tüm sakinler Avrupalı ya da hepsi Asyalı.” [114] Bunlar, modern yüklem mantığında kolayca ayırt edilir; burada birincinin ikinciyi takip ettiğini göstermek de mümkündür, ancak Boole sisteminde bunu temsil etmenin bir yolu olmaması önemli bir dezavantajdır. [115]
Onun içinde Sembolik Mantık (1881), John Venn sınıfları veya önermeler gerçeği koşulları arasında Boole ilişkileri ifade etmek çakışan alanlarının diyagramlar kullanılır. 1869’da Jevons, Boole’un yöntemlerinin mekanize edilebileceğini fark etti ve ertesi yıl Kraliyet Cemiyeti’ne gösterdiği “mantıksal bir makine” inşa etti.[112] 1885’te Allan Marquand, makinenin halen mevcut olan elektrikli bir versiyonunu önerdi.

Charles Sanders Peirce
Boole’un sistemindeki kusurların (varoluşsal önermeler için v harfinin kullanılması gibi) hepsi takipçileri tarafından giderildi. Jevons, 1864’te Pure Logic’i veya Nicelikten ayrı olarak Kalitenin Mantığını yayınladı; burada münhasır olanı veya Boole’un sisteminin büyük ölçüde basitleştirilmesine izin veren bir sembol önerdi.[116]
Bu, Schröder tarafından Vorlesungen’de (1890-1905) paralel sütunlarda teoremleri ortaya koyduğunda faydalı bir şekilde kullanıldı. Peirce (1880), tüm Boole seçmeli fonksiyonlarının tek bir ilkel ikili işlem kullanılarak nasıl ifade edilebileceğini gösterdi, “ne… ne de…” ve eşit derecede iyi “hem… hem de…”, [ 117] ancak, Peirce’in birçok yeniliği gibi, bu, Sheffer 1913’te yeniden keşfedene kadar bilinmeyen ya da fark edilmeden kaldı. [118] Boole’un ilk çalışması, Peirce (1867), Schröder (1877) ve Jevons’tan (1890) kaynaklanan mantıksal toplam fikrinden de yoksundur.), [119] ve ilk kez Gergonne (1816) tarafından önerilen ve Peirce (1870) tarafından açıkça ifade edilen dahil etme kavramı.

Boolean katları
Boole’un cebirsel sisteminin başarısı, tüm mantığın cebirsel temsil yeteneğine sahip olması gerektiğini ortaya koydu ve en iddialı olanı Schröder’in anıtsal Vorlesungen über die Algebra der Logik (“Lectures on the Algebra of Logic”, cilt iii 1895), ancak orijinal fikir Peirce tarafından yeniden öngörülmüştür. [120]
Boole’un Aristoteles‘in mantığını tereddütsüz kabul etmesi, mantık tarihçisi John Corcoran tarafından, Düşünce Yasalarına[121] erişilebilir bir girişte vurgulanmıştır. Corcoran ayrıca, Önceki Analizler ve Düşünce Yasaları’nın nokta nokta karşılaştırmasını da yazmıştır. [122]Corcoran’a göre Boole, Aristoteles‘in mantığını tamamen kabul etti ve onayladı. Boole’un hedefleri, Aristoteles‘in mantığının 1) ona denklemleri içeren matematiksel temeller sağlayarak, 2) tedavi edebileceği problem sınıfını genişletmek – geçerliliği değerlendirmekten denklemleri çözmeye – ve 3) aralığı genişletmek suretiyle “altına inmek, aşmak ve ötesine geçmek” idi. ele alabileceği uygulamaların sayısı ki örneğin, yalnızca iki terime sahip olan önermelerden, keyfi olarak çok sayıya sahip olanlara kadar.
Daha spesifik olarak Boole, Aristoteles‘indedim; Boole’un ‘anlaşmazlıkları’, eğer böyle adlandırılabilirlerse, Aristoteles‘in söylemediği şeyi ilgilendirir. Birincisi, temeller alanında Boole, Aristoteles mantığının dört önermesel biçimini denklem biçimindeki formüllere indirgedi ki bu başlı başına devrimci bir fikirdi. İkincisi, mantık problemleri alanında, Boole’un mantığa denklem çözme eklemesi – bir başka devrimci fikir olarak- Boole’un, Aristoteles‘in çıkarım kurallarının “mükemmel kıyaslamalar” denklem çözme kurallarıyla tamamlanması gerektiği doktrinini içeriyordu. Üçüncüsü, uygulamalar alanında, Boole’un sistemi çok terimli önermeleri ve argümanları ele alabilirken, Aristoteles yalnızca iki terimli özne-yüklem önermelerini ve argümanları ele alabilirdi. Örneğin, Aristoteles‘in sistemi bir sonuca varamadı “
MANTIKÇI DÖNEM

Gottlob Frege
Boole’den sonra, sonraki büyük gelişmeler Alman matematikçi Gottlob Frege tarafından yapıldı. Frege’nin amacı, Mantıkçılık programıdır, yani aritmetiğin mantıkla özdeş olduğunu göstermektir. [123] Frege, mantığa katı ve biçimsel yaklaşımında seleflerinin hepsinden çok daha ileri gitti ve hesabı veya Begriffsschrift önemlidir. [123] Frege ayrıca sayı kavramının tamamen mantıksal yollarla tanımlanabileceğini göstermeye çalıştı, böylece (eğer haklıysa) mantık, aritmetiği ve matematiğin aritmetiğe indirgenebilen tüm dallarını içerir. Bunu öneren ilk yazar o değildi. Öncü çalışması Die Grundlagen der Arithmetik’te (The Foundations of Arithmetic), 15–17. Bölümler, Leibniz, JS Mill ve Jevons’un çabalarını kabul ediyor ve Jevons’un “cebirin oldukça gelişmiş bir mantık ve sayı ancak mantıksal ayrımcılık olduğu” iddiasını öne sürüyor. [124]
Frege’nin ilk çalışması olan Begriffsschrift (“kavram senaryosu”), yalnızca iki bağlantıya (olumsuz ve koşullu), iki çıkarım kuralına (modus ponens ve ikame) ve altı aksiyoma dayanan, kesin bir şekilde aksiyomatize edilmiş bir önermesel mantık sistemidir. Frege, bu sistemin “tamlığına” atıfta bulundu, ancak bunu kanıtlayamadı.[125] Ancak en önemli yenilik, niceleyiciyi matematiksel işlevler açısından açıklamasıydı. Geleneksel mantık, “Sezar bir insandır” cümlesini temelde “bütün insanlar ölümlüdür” ile aynı biçimdedir. Özne adı olan tümceler, “her Sezar bir erkektir” şeklinde yorumlanabilen evrensel nitelikte kabul edildi. Başlangıçta Frege, geleneksel “konu ve yüklem” kavramlarını terk eder ve bunları sırasıyla argüman ve işlevle değiştirir ve bunun “zamanın testine dayanacağına inanır. Bir içeriği bir argümanın işlevi olarak değerlendirmenin nasıl yol açtığını görmek kolaydır. Ayrıca, kelimelerin anlamları arasındaki bağlantının gösterilmesi, eğer, değil, veya var, bazıları, hepsi ve benzeri, dikkati hak ediyor”. [127] Frege, “tüm erkekler” nicelik belirteci ifadesinin “tüm erkekler” ile aynı mantıksal veya anlamsal biçime sahip olmadığını ve evrensel önermenin “her A B’dir” olduğunu savundu.yani ‘- A’dır’ ve ‘- B’dir, öyle ki birinciyi ne olursa olsun ikinciyi de tatmin eder. Modern gösterimde bu şu şekilde ifade edilecektir:
İngilizce’de “tüm x’ler için, Ax ise Bx”. Bu nedenle, yalnızca tekil önermeler özne-yüklem biçimindedir ve indirgenemez bir şekilde tekildir, yani genel bir önermeye indirgenemez. Evrensel ve özel önermeler, aksine, hiç de basit özne-yüklem biçiminde değildir. Eğer “tüm memeliler”, “tüm memeliler kara sakinleridir” cümlesinin mantıksal öznesi olsaydı, tüm cümleyi reddetmek için “tüm memeliler kara canlıları değildir ” ifadesini reddetmemiz gerekirdi. Ancak durum bu değildi.[128] Sıradan dilde cümlelerin bu işlevsel analizi daha sonra felsefe ve dilbilim üzerinde büyük bir etkiye sahipti.
Bu, Frege’nin analizinde Boole’un “birincil” önermelerinin “ikincil” önermelerden farklı bir şekilde temsil edilebileceği anlamına gelir. “Bütün sakinler ya erkek ya da kadındır”
![]()
Frege’nin “Konsept Senaryosu”
oysa “Bütün sakinler erkek veya bütün sakinler kadındır”
Frege’nin Boole’un hesabının bir eleştirisinde belirttiği gibi:
- “Gerçek fark şu ki, [Boolean] ikiye bölmekten kaçınıyorum… ve partinin homojen bir sunumunu veriyorum. Boole’de iki parça yan yana çalışıyor, böylece biri diğerinin ayna görüntüsü gibi oluyor, ama tam da bu nedenle, onunla organik bir ilişkisi yoktur’ [129]
Frege’nin hesabı, birleşik ve kapsamlı bir mantık sistemi sağlamanın yanı sıra, eski çoklu genellik sorununu da çözdü. “Her kız çocuğu öptü” şeklindeki belirsizliğin geleneksel mantıkta ifade edilmesi zordur, ancak Frege’nin mantığı bunu nicelik belirteçlerinin farklı kapsamı aracılığıyla çözer. Böylece

Peano
her kıza, kızın öptüğü bir erkek (herhangi biri yapacak) karşılık geldiği anlamına gelir. Fakat
her kızın öptüğü belirli bir erkek çocuğu olduğu anlamına gelir. Bu cihaz olmasaydı, mantık projesi şüpheli veya imkansız olurdu. Frege bunu kullanarak atalardan kalma ilişkinin, çoka bir ilişkinin ve matematiksel tümevarımın bir tanımını sağladı. [130]
Bu dönem, Dedekind, Pasch, Peano, Hilbert, Zermelo, Huntington, Veblen ve Heyting’i içeren “matematik okulu” olarak bilinen çalışmalarla örtüşüyor. Amaçları, geometri, aritmetik, analiz ve küme teorisi gibi matematiğin dallarının aksiyomizasyonuydu. En dikkate değer olanı, tüm matematiği sınırlı bir aksiyomlar kümesine dayandırmaya çalışan, tutarlılığını “sonlu” araçlarla kanıtlayan ve herhangi bir matematiksel ifadenin doğruluğunu veya yanlışlığını belirleyecek bir prosedür sağlayan Hilbert’in Programı’ydı. Standart aksiyomlaştırılması arasında Doğal sayılar adlı Peano aksiyomlar eponymously. Peano, matematiksel ve mantıksal semboller arasında net bir ayrım sürdürdü. Frege’nin çalışmasından habersizken, mantıksal aygıtını Boole ve Schröder’in çalışmalarına dayanarak bağımsız olarak yeniden yarattı. [131]

Ernst Zermelo (1871-1953
Mantıkçı proje, 1901’de Bertrand Russell tarafından bir paradoksun keşfedilmesiyle neredeyse ölümcül bir gerileme yaşadı. Bu, Frege’nin saf küme teorisinin bir çelişkiye yol açtığını kanıtladı. Frege’nin teorisi, herhangi bir biçimsel kriter için, kriteri karşılayan tüm nesnelerin bir takım olduğu aksiyomunu içeriyordu. Russell, tam olarak kendi üyesi olmayan kümeleri içeren bir kümenin kendi tanımıyla çelişeceğini gösterdi (eğer kendisinin bir üyesi değilse, kendisinin bir üyesidir ve kendisinin bir üyesi ise değildir). [132] Bu çelişki artık Russell paradoksu olarak biliniyor. Bu paradoksu çözmenin önemli bir yöntemi Ernst Zermelo tarafından önerildi.[133] Zermelo küme teorisiilk aksiyomatik küme teorisiydi. Artık kanonik olan Zermelo-Fraenkel küme teorisine (ZF) geliştirildi. Russell’ın paradoksu sembolik olarak şu şekildedir:
Russell ve Alfred North Whitehead tarafından yazılan ve 1910-13’te yayınlanan matematiğin temelleri üzerine üç ciltlik bir çalışma olan anıtsal Principia Mathematica, paradoksu ayrıntılı bir türler sistemi aracılığıyla çözme girişimini de içeriyordu : bir dizi öğe her bir öğesinden farklı bir türdedir (küme, öğe değildir; bir öğe küme değildir) ve “tüm kümeler kümesi” nden söz edilemez. Principia bir iyi tanımlanmış kümesinden tüm matematiksel gerçekleri türetmek girişimiydi aksiyomları ve çıkarsama kuralları içinde sembolik mantık.
MATEMATİK DÖNEM

Kurt Gödel
İsimleri Gödel ve Tarski 1930’lar hakim,[134] gelişiminde önemli bir dönem Metamatematik – üretmek için matematiksel yöntemler kullanılarak matematik çalışma metatheories veya diğer matematiksel teorileri hakkında matematiksel teorileri. Metamatematikle ilgili ilk araştırmalar Hilbert’in programı tarafından yönlendirilmişti. 1929 yılında verilen bir göstermiştir Gödel, çalışmalarında sonuçlandı Metamatematik üzerindeki çalışmalar birinci dereceden cümle ise anlaşılabilir ve eğer mantıklı geçerlidir olursa – ki her doğrudur yani yapının kendi dil için. Bu Gödel’in tamlık teoremi olarak bilinir. Bir yıl sonra, Hibert’in programının orijinal haliyle ulaşılamaz olduğunu gösteren iki önemli teoremi kanıtladı. Birincisi, teoremleri bir algoritma veya bilgisayar programı gibi etkili bir prosedürle listelenebilen hiçbir tutarlı aksiyom sistemi, doğal sayılarla ilgili tüm gerçekleri kanıtlayamaz. Bu tür herhangi bir sistem için, her zaman doğru olan ancak sistem içinde kanıtlanamayan doğal sayılarla ilgili ifadeler olacaktır. İkincisi, eğer böyle bir sistem aynı zamanda doğal sayılarla ilgili bazı temel gerçekleri ispatlayabiliyorsa, sistemin kendisinin tutarlılığını kanıtlayamayacağıdır. Bu iki sonuç Gödel’in eksiklik teoremleri olarak bilinir veya basitçeGödel’in Teoremi. On yılın ilerleyen zamanlarında Gödel, seçim aksiyomunun ve süreklilik hipotezinin Zermelo-Fraenkel küme teorisi ile tutarlı olduğunun ispatının bir parçası olarak küme-teorik inşa edilebilirlik kavramını geliştirdi. Gelen geçirmez teori, Gerhard Gentzen geliştirilen doğal kesinti ve sıralı kalkülüs. Birincisi, pratikte ‘doğal olarak’ meydana geldiği için mantıksal akıl yürütmeyi modellemeye çalışır ve en kolay şekilde sezgisel mantığa uygulanır, ikincisi ise herhangi bir biçimsel sistemde mantıksal ispatların türetilmesini açıklığa kavuşturmak için tasarlanmıştır. Gentzen’in çalışmasından bu yana, doğal tümdengelim ve ardışık taşlar ispat teorisi, matematiksel mantık ve bilgisayar bilimi alanlarında yaygın olarak uygulanmaktadır. Gentzen ayrıca mantıksal ispatları normal bir forma indirgemek için kullanılabilecek sezgisel ve klasik mantık için normalleştirme ve kesme-eliminasyon teoremlerini de kanıtladı. [135] [136]

Alfred Tarski
Łukasiewicz’in öğrencisi olan Alfred Tarski, en iyi gerçeği ve mantıksal sonucu tanımlaması ve mantıksal tatmin anlamsal kavramı ile bilinir. 1933’te, anlamsal doğruluk teorisini önerdiği resmi dillerde doğruluk kavramını (Lehçe) yayınladı: “kar beyazdır” gibi bir cümle, ancak ve ancak kar beyazsa doğrudur. Tarski’nin teorisi, hakikatle ilgili ifadeyi yapan metal dili, doğruluğu ileri sürülen cümleyi içeren nesne dilinden ayırdı ve bir yazışma ( T-şeması) verdi.) nesne dilindeki ifadeler ile bir yorumun unsurları arasında. Tarski’nin gerçeği açıklamanın zor fikrine yaklaşımı, özellikle model teorisinin geliştirilmesinde mantık ve felsefede kalıcı bir şekilde etkili olmuştur. [137] Tarski ayrıca tümdengelimli sistemlerin metodolojisi ve bütünlük, karar verilebilirlik, tutarlılık ve tanımlanabilirlik gibi temel ilkeler üzerine önemli çalışmalar yaptı. Anita Feferman’a göre Tarski, “yirminci yüzyılda mantığın çehresini değiştirdi”. [138]
Alonzo Church ve Alan Turing, sırasıyla 1936 ve 1937’de Hilbert’in Entscheidungsproblem’ine bağımsız negatif çözümler sunan biçimsel hesaplanabilirlik modelleri önerdiler. Entscheidungsproblem herhangi bir resmi matematiksel ifadesi göz önüne alındığında, algoritmik ifade doğrudur belirleyecek, bir prosedür istedi. Church ve Turing böyle bir prosedür olmadığını kanıtladı; Turing’in makalesi, durdurma problemini, algoritmik bir çözümü olmayan matematiksel bir problemin anahtar bir örneği olarak tanıttı.
Church’ün hesaplama sistemi modern λ-kalkülüsüne dönüşürken, Turing makinesi genel amaçlı bir hesaplama cihazı için standart bir model haline geldi. Kısa süre sonra, önerilen diğer birçok hesaplama modelinin, Church ve Turing tarafından önerilenlere eşdeğer güçte olduğu gösterildi. Bu sonuçlar Church-Turing tezine, bir insan tarafından gerçekleştirilebilecek herhangi bir deterministik algoritmanın bir Turing makinesi ile gerçekleştirilebileceği tezine yol açtı. Kilise hem gösteren, ek kararlaştırılamazlık sonuçlarını kanıtladı Peano aritmetik ve birinci dereceden mantık vardır undecidable. Daha sonra Emil Post ve Stephen Cole Kleene’nin çalışmaları1940’larda hesaplanabilirlik teorisinin kapsamını genişletti ve çözülemezlik dereceleri kavramını tanıttı.
Yirminci yüzyılın ilk birkaç on sonuçları da üzerinde bir etkisi oldu analitik felsefe ve felsefi mantık, özellikle gibi konularda, 1950’lerden sonra modal mantık, zamansal mantık, dışsal bir mantık ve alaka mantığı.
İKİNCİ DÜNYA SAVAŞI VE SONRASINDA MANTIK

Saul Kripke
II.Dünya Savaşı’ndan sonra matematiksel mantık birbiriyle ilişkili ancak ayrı araştırma alanlarına ayrıldı: model teorisi, ispat teorisi, hesaplanabilirlik teorisi ve küme teorisi. [139]
Küme teorisinde, zorlama yöntemi, modeller oluşturmak ve bağımsızlık sonuçları elde etmek için sağlam bir yöntem sağlayarak alanda devrim yarattı. Paul Cohen bağımsızlığını kanıtlamak için 1963 yılında bu yöntemi tanıtıldı süreklilik hipotezinin ve seçme aksiyomu gelen Zermelo-Fraenkel küme kuramı.[140] Girişinden kısa bir süre sonra basitleştirilen ve genişletilen tekniği, o zamandan beri matematiksel mantığın tüm alanlarında başka birçok soruna uygulandı.
Hesaplanabilirlik teorisinin kökleri 1930’larda ve 40’larda Turing, Church, Kleene ve Post’un çalışmalarına dayanıyordu. Özyineleme teorisi olarak bilinen soyut hesaplanabilirlik çalışmasına dönüştü.[141] öncelikli yöntemi ile, bağımsız bir şekilde keşfedilen Albert Muchnik ve Richard Friedberg anlaşılmasında önemli gelişmelere yol açmıştır, 1950’lerde unsolvability dereceleri ve ilgili yapıların. Yüksek mertebeden hesaplanabilirlik teorisi üzerine yapılan araştırmalar, teorinin set teorisiyle bağlantılarını gösterdi. Yapıcı analiz ve hesaplanabilir analiz alanlarıklasik matematik teoremlerinin etkili içeriğini incelemek için geliştirilmiştir; bunlar sırayla ters matematik programına ilham verdi. Hesaplanabilirlik teorisinin ayrı bir dalı olan hesaplama karmaşıklığı teorisi de, tanımlayıcı karmaşıklığa yönelik araştırmaların bir sonucu olarak mantıksal terimlerle karakterize edildi.
Model teorisi, belirli matematiksel teorilerin modellerini incelemek için matematiksel mantık yöntemlerini uygular. Alfred Tarski, adını model teorisine katkılar başlığı altında yayınladığı bir dizi makaleden alan bu alanda öncü çalışmalar yayınladı. 1960’larda Abraham Robinson, ilk kez Leibniz tarafından önerilen bir problem olan sonsuz küçüklere dayalı analiz ve analiz geliştirmek için model-teorik teknikler kullandı.
Kanıt teorisinde, klasik matematik ile sezgisel matematik arasındaki ilişki, Georg Kreisel tarafından icat edilen gerçekleştirilebilirlik yöntemi ve Gödel’in Dialectica yorumu gibi araçlarla açıklığa kavuşturuldu. Bu çalışma, kanıt madenciliğinin çağdaş alanına ilham verdi. Curry-Howard yazışma doğal kesinti sistemleri arasında bir yazışma dahil mantık ve hesaplama arasındaki derin benzetme olarak ortaya Yazılan lamda kalıkuli bilgisayar bilimlerinde kullanılır. Sonuç olarak, bu biçimsel sistemler sınıfına yönelik araştırmalar hem mantıksal hem de hesaplama yönlerini ele almaya başladı; bu araştırma alanı modern tip teori olarak bilinmeye başladı. Sıralı analizde ve Paris-Harrington teoremi gibi aritmetikte bağımsızlık sonuçlarının incelenmesinde de ilerlemeler kaydedildi.
Bu aynı zamanda, özellikle 1950’lerde ve sonrasında, matematiksel mantık fikirlerinin felsefi düşünceyi etkilemeye başladığı bir dönemdi. Örneğin, gergin mantık, zaman açısından nitelendirilen önermeleri temsil etmek ve bunlar hakkında akıl yürütmek için biçimlendirilmiş bir sistemdir. Filozof Arthur Prior, 1960’lardaki gelişiminde önemli bir rol oynadı. Modal mantık, biçimsel mantığın kapsamını modalite unsurlarını (örneğin, olasılık ve gereklilik ) içerecek şekilde genişletir. Saul Kripke’nin, özellikle olası dünyalar ve artık Kripke semantiği olarak adlandırılan biçimsel sistem hakkındaki fikirlerianalitik felsefe üzerinde derin bir etkiye sahiptir. [142] En iyi bilinen ve en etkili eseri Naming and Necessity’dir (1980). [143] Deontik mantık, modal mantıkla yakından ilişkilidir: zorunluluk, izin ve ilgili kavramların mantıksal özelliklerini yakalamaya çalışırlar. Bazı temel yenilikler rağmen syncretizing matematiksel ve felsefi mantık tarafından gösterildi Bolzano 1800’lü yılların başında, öyleydi Ernst Mally, öğrencisi Aleksios Meinong yaptığı ilk resmi dışsal bir sistemin önerilmesi oldu Grundgesetzenin des Sollens, Whitehead ve Russell’ın önerme analizinin sözdizimine dayanmaktadır.
II.Dünya Savaşı’ndan sonra kurulan bir diğer mantıksal sistem ise 1965 yılında Azerbaycanlı matematikçi Lotfi Asker Zadeh tarafından bulanık mantıktı.
KAYNAKÇA
KAYNAKLAR
|
















