İlişkili Legendre Polinomları

İlişkili Legendre polinomları genel Legendre denklemi içerisinde kanonik çözümlerdir

(1-x ^ {2}) {\ frac {d ^ {2}} {dx ^ {2}}} P _ {\ ell} ^ {m} (x) -2x {\ frac {d} {dx} } P _ {\ ell} ^ {m} (x) + \ sol [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P_ {\ ell} ^ {m} (x) = 0

,

Veya eşdeğer olarak

${\ frac {d} {dx}} \ left [(1-x ^ {2}) {\ frac {d} {dx}} P _ {\ ell} ^ {m} (x) \ sağ] + \ left [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P _ {\ ell} ^ {m} (x) = 0$ ,

burada ℓ ve m (tamsayılar) endekslerine sırasıyla ilgili Legendre polinomunun derecesi ve sırası denir. Bu denklem, yalnızca ℓ ve m , 0 ≤ m ≤ inte veya tam olarak eşdeğer negatif değerlerle tamsayılarsa , [−1, 1] ‘de tekil olmayan çözümler içerir . Ek olarak m eşit olduğunda, fonksiyon bir polinomdur . Tüm m, sıfır ve ℓ tamsayıdır, bu fonksiyonlar aynıdır Legendre polinomları . ℓ ve ne zaman Genelde m tamsayılar, düzenli çözümler bazen denilen onlar olmasa bile, “Legendre polinomları ilişkili” olan vardır polinomları zamanm tuhaf. Rasgele gerçek veya ℓ ve kompleks değerler ile fonksiyonların tamamen genel bir sınıfı m olan Legendre fonksiyonları . Bu durumda parametreler genellikle Yunanca harflerle etiketlenir.

Legendre adi diferansiyel denklemine fizik ve diğer teknik alanlarda sıkça rastlanır . Özellikle, küresel koordinatlarda Laplace denklemini (ve ilgili kısmi diferansiyel denklemleri ) çözerken ortaya çıkar . İlişkili Legendre polinomları, küresel harmoniklerin tanımlanmasında hayati bir rol oynar .

Negatif olmayan tamsayı parametrelerinin tanımı ℓ ve m

Bu işlevler $P _ {\ ell} ^ {m} (x)$ , üst simge P’nin gücünü değil sırası belirtir . En açık tanımları sıradan Legendre polinomlarının türevleri ( m ≥ 0)

${\ displaystyle P _ {\ ell} ^ {m} (x) = (- 1) ^ {m} (1-x ^ {2}) ^ {m / 2} {\ frac {d ^ {m}} { dx ^ {m}}} \ sol (P _ {\ ell} (x) \ sağ)}$ ,

Bu formülde (−1) ^m faktörü, Condon – Shortley fazı olarak bilinir . Bazı yazarlar bunu atlıyor. Bu denklem ile tanımlanan fonksiyonlar parametreleri ℓ belirtilen değerler genel Legendre diferansiyel denklemi yerine ve m farklılaşarak aşağıdaki m kez Legendre denklemi P _ℓ : ^[1]

(1-x ^ {2}) {\ frac {d ^ {2}} {dx ^ {2}}} P _ {\ ell} (x) -2x {\ frac {d} {dx}} P _ {\ ell} (x) + \ ell (\ ell +1) P _ {\ ell} (x) = 0.

Üstelik Rodrigues formülü ile ,

P _ {\ ell} (x) = {\ frac {1} {2 ^ {\ ell} \, \ ell!}} \ {\ Frac {d ^ {\ ell}} {dx ^ {\ ell}}} \ left [(x ^ {2} -1) ^ {\ ell} \ right],

P ^m
_ℓ şeklinde ifade edilebilir

$P _ {\ ell} ^ {m} (x) = {\ frac {(-1) ^ {m}} {2 ^ {\ ell} \ ell!}} (1-x ^ {2}) ^ {m / 2} \ {\ frac {d ^ {\ ell + m}} {dx ^ {\ ell + m}}} (x ^ {2} -1) ^ {\ ell}.$

Bu denklem m aralığının genişletilmesine izin verir : −ℓ ≤ m ≤ ℓ. Tanımları P _ℓ^± m ± ikamesi ile, bu ifadesi sonucu elde edilen, m , orantılıdır. Gerçekten de, eşit güçlerin katsayılarını sol ve sağ taraftaki

{\ frac {d ^ {\ ell -m}} {dx ^ {\ ell -m}}} (x ^ {2} -1) ^ {\ ell} = c_ {lm} (1-x ^ {2 }) ^ {m} {\ frac {d ^ {\ ell + m}} {dx ^ {\ ell + m}}} ​​(x ^ {2} -1) ^ {\ ell},

o zaman orantılılık sabitinin

$c_ {lm} = (- 1) ^ {m} {\ frac {(\ ell -m)!} {(\ ell + m)!}},$

Böylece

$P _ {\ ell} ^ {- m} (x) = (- 1) ^ {m} {\ frac {(\ ell -m)!} {(\ Ell + m)!}} P _ {\ ell} ^ {m} (x) tanımlanmaktadır.$

Alternatif gösterimler

Literatürde aşağıdaki alternatif gösterimler de kullanılmaktadır: ^[2]

$P _ {\ ell m} (x) = (-1) ^ m P_ \ ell ^ {m} (x)$

Kapalı Form

Associated Legendre Polinomu ayrıca şu şekilde de yazılabilir:

${\ displaystyle P_ {l} ^ {m} (x) = (- 1) ^ {m} \ cdot 2 ^ {l} \ cdot (1-x ^ {2}) ^ {m / 2} \ cdot \ toplam _ {k = m} ^ {l} {\ frac {k!} {(km)!}} \ cdot x ^ {km} \ cdot {\ binom {l} {k}} {\ binom {\ frac {l + k-1} {2}} {l}}}$

Diklik

0 ≤ m ≤ ℓ olduğu varsayılarak , sabit m için diklik koşulunu yerine getirirler :

\ int _ {- 1} ^ {1} P_ {k} ^ {m} P _ {\ ell} ^ {m} dx = {\ frac {2 (\ ell + m)!} {(2 \ ell +1 ) (\ ell -m)!}} \ \ delta _ {k, \ ell}

Δ _{k olduğunda} , the Kronecker deltasıdır .

Ayrıca, sabit ort için diklik koşulunu yerine getirirler:

\ int _ {- 1} ^ {1} {\ frac {P _ {\ ell} ^ {m} P _ {\ ell} ^ {n}} {1-x ^ {2}}} dx = {\ begin { durumlar} 0 & {\ mbox {if}} m \ neq n \\ {\ frac {(\ ell + m)!} {m (\ ell -m)!}} & {\ mbox {if}} m = n \ neq 0 \\\ hırsızlık & {\ mbox {if}} m = n = 0 \ end {cases}}

Negatif m ve / veya negatif edit

Diferansiyel denklem, m işaretindeki bir değişiklik altında açıkça değişmez .

Negatif m fonksiyonlarının yukarıda pozitif m fonksiyonlarıyla orantılı olduğu gösterilmiştir :

$P _ {\ ell} ^ {- m} = (- 1) ^ {m} {\ frac {(\ ell -m)!} {(\ Ell + m)!}} P _ {\ ell} ^ {m}$

(Bu, Rodrigues’in formül tanımından kaynaklanmıştır. Bu tanım, çeşitli yineleme formüllerinin pozitif veya negatif m için çalışmasını sağlar .)

${\ textrm {If}} \ quad {\ mid} m {\ mid}> \ ell \, \ quad \ mathrm {then} \ quad P _ {\ ell} ^ {m} = 0. \,$

Diferansiyel denklem de ℓ ile −ℓ – 1 arasında bir değişimle değişmez ve negatif ℓ işlevleri şu şekilde tanımlanır:

$P _ {- \ ell} ^ {m} = P _ {\ ell -1} ^ {m}, \ (\ ell = 1, \, 2, \, ...)$ .

Eşlik

Tanımlarından, Associated Legendre işlevlerinin aşağıdakilere göre eşit veya tek olduğunu doğrulayabilir

P _ {\ ell} ^ {m} (- x) = (- 1) ^ {\ ell + m} P _ {\ ell} ^ {m} (x)

İlişkilendirilmiş ilk Legendre işlevleri

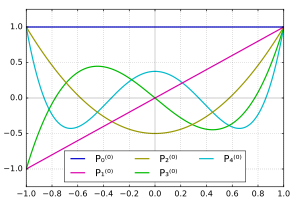
M = 0 için İlişkili Legendre işlevleri

İlişkili Legendre Polinomları

Negatif olmayan tamsayı parametrelerinin tanımı ℓ ve m

Alternatif gösterimler

Kapalı Form

Diklik

Negatif m ve / veya negatif edit

Eşlik

İlişkilendirilmiş ilk Legendre işlevleri

Yineleme formülü

Gaunt’un formülü

Hipergeometrik fonksiyonlarla genelleme

Açı bakımından yeniden parametrelendirme

Fizikteki uygulamalar: küresel harmonikler

Genellemeler

Notlar ve referanslar

${\ frac {1} {2}} \ int _ {- 1} ^ {1} P_ {l} ^ {u} (x) P_ {m} ^ {v} (x) P_ {n} ^ {w } (x) dx =$	$(-1) ^ {smw} {\ frac {(m + v)! (N + w)! (2s-2n)! S!} {(Mv)! (Sl)! (Sm)! (Sn)! (2s + 1)!}}$
	$\ times \ \ sum _ {t = p} ^ {q} (- 1) ^ {t} {\ frac {(l + u + t)! (m + somun)!} {t! (lut)! ( m-n + u + t)! (KSK)!}}$